Exercices: Les suites

démontrer que la série de terme général: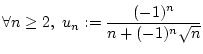

est convergente

1)Montrer que pour tout n appartenant à N , nous avons X(n) unique dans [0 ;1] :

n X(n)+ X(n)^ (3) = n

2) montrer que X(n) est croissante

3) montrer que X(n) est convergente

4) montre que 1-1/n ≤ x(n)≤1 que soit n appartenant à N –{0}

5) en déduire que lim x(n) quand x-> +∞

calculez la limite de Wn en +00 tel que ;



bonne chance

Soit J_n suite définie par:

trouver la limite de J_n(n-->+00)

une question interessante ^^

Dans la plupart des exos,ou on vous donne une suite (u_n) dans une question on dit:soit la suite (v_n) définie par: et on donne une expression de (v_n) en fonction de (u_n).
Puis on dit démontrer que (v_n) est une suite géométrique (ou arithmétique) pour enfin déduire l'expression de(u_n)

La question est:

celui (ou celle ^^) qui a posé l'exo,comment a-t-il pensé à l'expression de (v_n) en fonction de (u_n) qu'il a donné ?

Ma réponse est:
bon c'est une theoreme.

Si on a : U(n+2)=a.U(n+1)+b.Un
on cherche la solution de: X²-aX-b=0
- si on a trouvé deux solutions r et r'
alors il existe deux suites telle que:
Vn=U(n+1)-r.Un et Wn= U(n+1)-r'.Un
et on déduit que:
existe m et p dans IR telle que: Un=m.(r)^n+p(r')^n
-si on a trouvé une seule solution r
alors il existe deux suites telle que:
Tn=U(n+1)-r.Un et Sn=Un/Tn
et on déduit que:
existe m et p dans IR telle que: Un=(m.n+p).r^n
(vous pouvez demontrer tout ça)

Si on a : U(n+1)=a.Un +b
on cherche la fonction f telle que : f(Un)=U(n+1)
alors on résout l'équation f(x)=x
-si on a trouvé une seule solution r on pose:
Vn=Un-r
-si on atrouvé deux solution r et r' on pose :
Wn=(Un-r)/(Un-r')

(tout va bien maintenant)
bonne chance

considerons la suite U(n+1)= (1/2)Un + (1/2)a²
Calculez la limite de cette suite (Un)n£IN.

soit Un une suite definie par:

Un+2=Un+1 + Un + 1 (n £ IN)

u0=3 et u1=1

determiner Un en fonction de n

calculer lim Un+1/ Un

démontrer que la suite définie par: est croissante à partir d'un certain rang N.

(Vn) et (Un) deux suite tels que qqsoit n de N
Un< a et Vn<b /a et b de R
on a limVn+Un=a+b
montrer que lim Vn=b et lim Un=a

je propose cet éxercice pour les élèves de terminal SM seulement.
(si vous séchez aprés avoir chercher la solution sera posté..)
.
a_1=1 a_n+1=1/16[1+4a_n+sqrt(1+24a_n)].
et (b_n)² =1+24a_n.
1- montrer que b_(n+1) -3 = 1/2[b_n -3].
2- en deduire a_n en fonction de n.
bon courage .sqrt(x)=racine de x.
aissa.

Soit un une suite definie tel que :
u1=1 Un= ( 1/nV(n) )(sigma de racine k ; k varie de 1 jusq n ) N>=2

montrer que la limite de Un = 2/3 vous pouvez considerez la fonction

F:x------> 2/3x^2/3 et appliquer TAf sur l'intervale [k K+1 ]

exercice 1

Depuis qu'il est à la retraite, un homme tond sa pelouse tous les samedis, il recueille chaque fois 120 litres de gazon qu'il stocke dans un bac à compost de 300 litres.
Chaque semaine les matières stockées perdent, après décomposition ou prélèvement les trois quarts de leur volume.
Soit V1, V2, V3 les volumes en litres stockés respectivement les premier, deuxième et troisième samedis après la tonte.
De manière générale, soit Vn le volume stocké le nième samedi après la tonte.
1. a) Montrer que V1 = 120 litres, V2 = 150 litres, V3 = 157,5 litres.
b) Calculer les volumes V4, V5, V6 exprimés en litres, stockés respectivement les quatrième, cinquième, sixième samedis après la tonte.
2. Exprimer Vn+1 en fonction de Vn.
3. On définit, pour tout n1, tn par : tn = 160 - Vn.
a) Montrer que (tn) est la suite géométrique de premier terme t1 = 40 et de raison .
b) En déduire les expressions de tn puis de Vn en fonction de n.
c) Déterminer la limite de (tn) puis celle de (Vn).


exercice 2

Au premier janvier 1995, une ville A compte 200 000 habitants. A la même date une ville B a 150 000 habitants.
On a constaté que la population de la ville A diminue de 3% par an et que celle de la ville B augmente de 5% par an.
Dans cet exercice, on suppose que les croissances et les diminutions se poursuivent à ce rythme.
1. Quelles seront les populations des villes A et B au premier janvier 1996 ? au premier janvier 1997 ?
2. Pour tout entier n, on désigne par : an la population de la ville A au premier janvier de l'année (1995 + n) et par bn la population de la ville B à la même date.
a) Vérifier que les suites (an) et (bn) sont géométriques. Préciser leurs raisons respectives.
b) Exprimer an et bn en fonction de n.
c) Au premier janvier de cette année, la population de la ville B sera-t-elle, pour la première fois, supérieure à celle de la ville A ?

Exercice 1 :

I - On considère la suite (Un) où n£IN* définie par U1=1 et, pour tout n£IN* ,
U indice (n+1) : Un+1 = n/[2(n+1)]*Un + [3(n+2)]/[2(n+1)]

1) Démontrer que cette suite est majorée par 3.
2) Démontrer que cette suite est monotone (étudier directement le signe de Un+1 - Un)
3) Démonter que cette suite est convergente. Calculer sa limite.

1) J'ai su faire (récurrence).
2) Je ne vois pas comment trouver Un
3) La suite est majorée et croissante donc convergente. Il faut avoir Un pour faire le calcul de la limite? (car lim Un = lim Un+1 donc l=....)


II - On considère la suite (Vn) où n£IN* définie pour tout n£IN* par Vn = n(3-Un)

1) Démontrer que cette suite est une suite géométrique dont on précisera le premier terme et la raison.
2) Exprimer Vn puis Un en fonction de n. Retrouver la limite de la suite (Un) où n£IN*

1) Vn+1 = (n+1)(3-(Un+1)) je coince sur le calcul
2) Vn = Vo*q^n = n(3-Un) ?
Un = (3n - Vo*q^n)/n ?


Exercice 2 : VRAI ou FAUX

Vraie => justification rapide
Faux => contre-exemple
Pour toutes suites numériques (Un) où n£IN* et (Vn) où n£IN* telles ques, pour tout n£IN* , Un différe à 0,
on a :

a) Si (Un+Vn) converge vers 1, alors (Un) et (Vn) sont convergentes.
b) Si (Un) et (Vn) convergent vers 1, alors (Un/Vn) converge vers une limite finie.
c) Si (Vn) converge vers 0 et (Un/Vn) vers 1, alors (Un) converge vers 0.
d) Si (|Vn|) est convergente, alors (Vn) est convergente.